How Is Your Knowledge of Electromagnetic Field Theory, Soddy Circles, and Circle Packing Theory? Fortunately Acushnet’s Golf Ball Engineers Know a Little About These Subjects

An interesting golf ball patent issued yesterday to Acushnet. The patent is USPN 7473194 titled “Dimpled Golf Ball and Dimple Distributing Method” and describes the invention as:

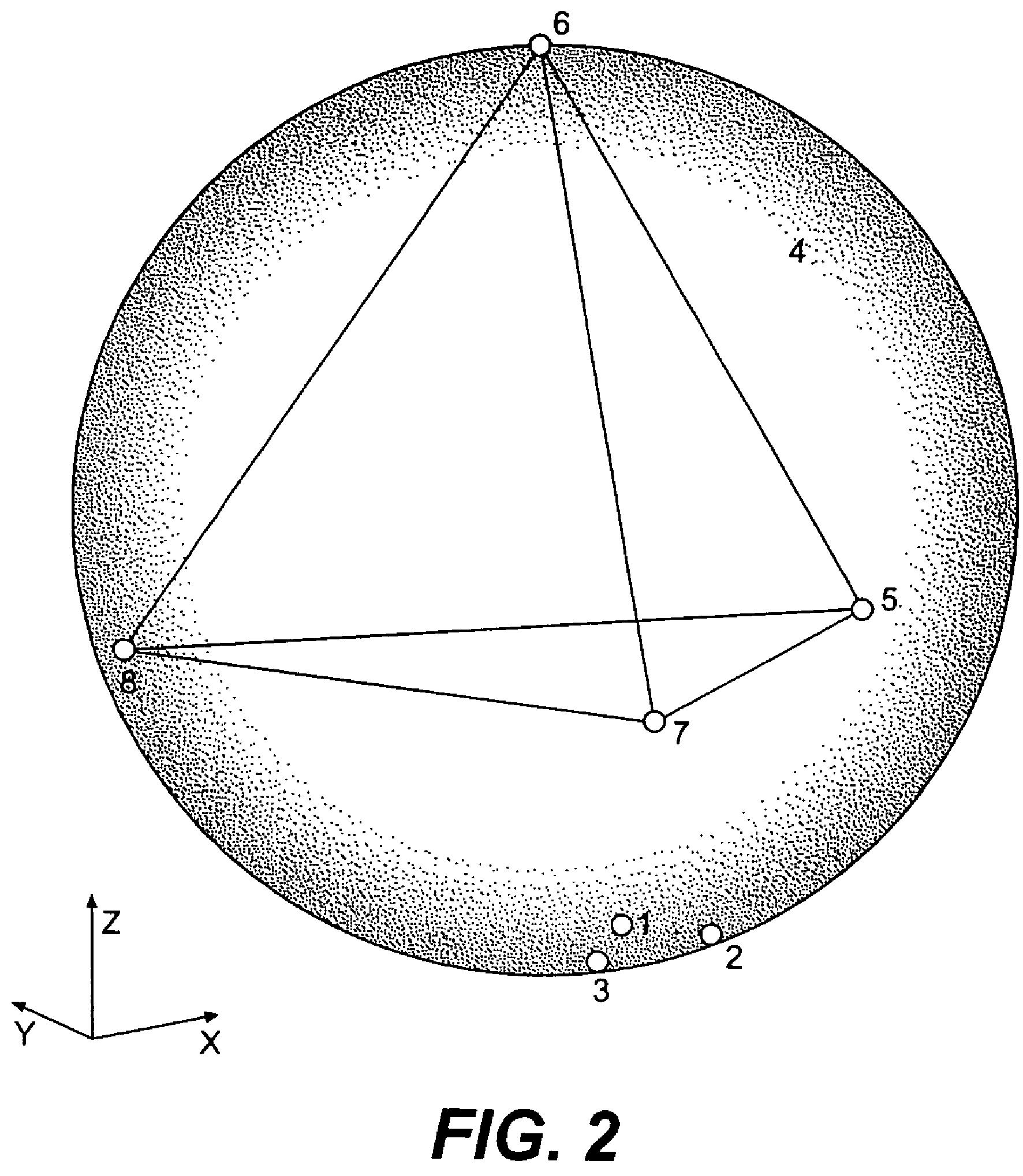
A golf ball having a plurality of dimples on its surface, the dimples as a whole are distributed on at least a portion of the golf ball based on Soddy circles. The portion of the golf ball may be triangulated, and Soddy circles may be generated based on the vertices of each triangle. Dimples may then be arranged according to the generated Soddy circles. Alternately, dimples within the portion of the golf ball may be distributed based on circle packing.

Like most golf ball dimple related patents, it is full of interesting information. For instance….

A number of physical phenomena are described by Laplace’s equation including steady-state heat conduction, incompressible fluid flow, elastostatics, as well as gravitational and electromagnetic fields. The theory of solutions of this equation is called Potential Theory.

One example of Potential Theory is electromagnetic field theory, which can be used to distribute objects on a spherical surface. Electromagnetic field theory has been studied extensively over the years for a variety of applications. It has been used, for example, in satellite mirror design. Electromagnetic field theory, including the obvious applications to semiconductor research and computer technology, has many applications in the physical sciences, not limited to celestial mechanics, organic chemistry, geophysics, and structural acoustics.

In many applications, the objects are treated as point charges so that principles of electromagnetic field theory can be applied to determine optimal positioning or to predict the equilibrium position of the objects.

While the task of distributing point charges on a spherical surface has been studied extensively in mathematical circles, it has not been employed as a tool to develop and define dimple patterns or optimal dimple distributions on a golf ball.

Instead, current golf ball dimple patterns generally are based upon dividing the spherical surface of the ball into discrete polygonal surfaces. The edges of the surfaces join to form geometric shapes that approximate the spherical surface of a golf ball. These geometric shapes include, for example, regular octahedral, regular icosahedral and regular polyhedral arrangements. Once a geometric shape is selected, the polyhedral surfaces are individually filled with a dimple pattern that may be repeated over the surface.

While this approach may be effective in enabling easy dimple design and mold manufacture, it may not result in optimal dimple positioning or distribution for improved aerodynamic performance. In addition, this approach to designing a dimple pattern may result in a golf ball having variations in flight performance depending upon the direction of rotation of the ball. For instance, rotation about one axis may result in different flight characteristics than rotation about a second axis. Moreover, the difference may be large enough to produce a measurable and visible difference in aerodynamic lift and drag.

The potential limitations described above may be present in other methods for arranging dimples on a golf ball. Thus, it would be desirable to have a way to optimize a dimple pattern by repositioning the dimples to improve flight performance.

SUMMARY OF THE INVENTION

The present invention uses electromagnetic field theory to create dimple patterns and to optimize dimple placement and distribution on a golf ball. The method solves the constrained optimization problem where the objective function is an electric potential function subject to various constraints imposed, such as dimple spacing or size. A number of potential functions can be utilized to describe the point charge interactions. A variety of optimization methods are available to minimize the objective function including gradient based, response surface, and neural network algorithms. These solution strategies are readily available and known to one skilled in the art. One embodiment of the present invention uses a Coulomb potential function and a gradient based solution strategy to create a dimple pattern. One benefit from using these principles to develop dimple patterns is that doing so may result in a golf ball having improved aerodynamic performance.

Use of the inventive method provides a golf ball having a plurality of dimples on its surface, some of which have been positioned on the golf ball surface according to principles of electromagnetic theory. At first, the dimples that are to be positioned according to these principles may be randomly distributed on at least a portion of the golf ball surface. The ball surface may be divided into hemispheres, quadrants, or according to platonic solid shapes in order to define the portion of the golf ball on which the dimples will be arranged.

In one embodiment, the dimples are placed on a hemispherical portion of the golf ball. In another embodiment, the dimples are placed on the entire spherical portion of the ball. In yet another embodiment, the dimples are placed on the regions defined by an Archimedean solid, most preferably a great rhombicosidodecahedron.

The dimples may have any desired shape, although in a preferred embodiment the dimples are circular. In another embodiment, however, the dimples are polygonal in shape. In addition the dimples may be of any desired number. In one embodiment, the dimples are between about 200 to about 600 in number. In a preferred embodiment, the dimples are between about 300 to about 500 in number.

The size of the dimples may also vary. In one embodiment, the dimples are between about 0.04 to about 0.1 inches when measured from the centroid of the dimple to its outermost extremity. More preferably, the dimples are about 0.05 to about 0.09 inches in size. In yet another embodiment, the dimples are substantially circular and have varying diameters sizes from about 0.04 to about 0.20 inches, and more preferably are between about 0.100 and about 0.180 inches.

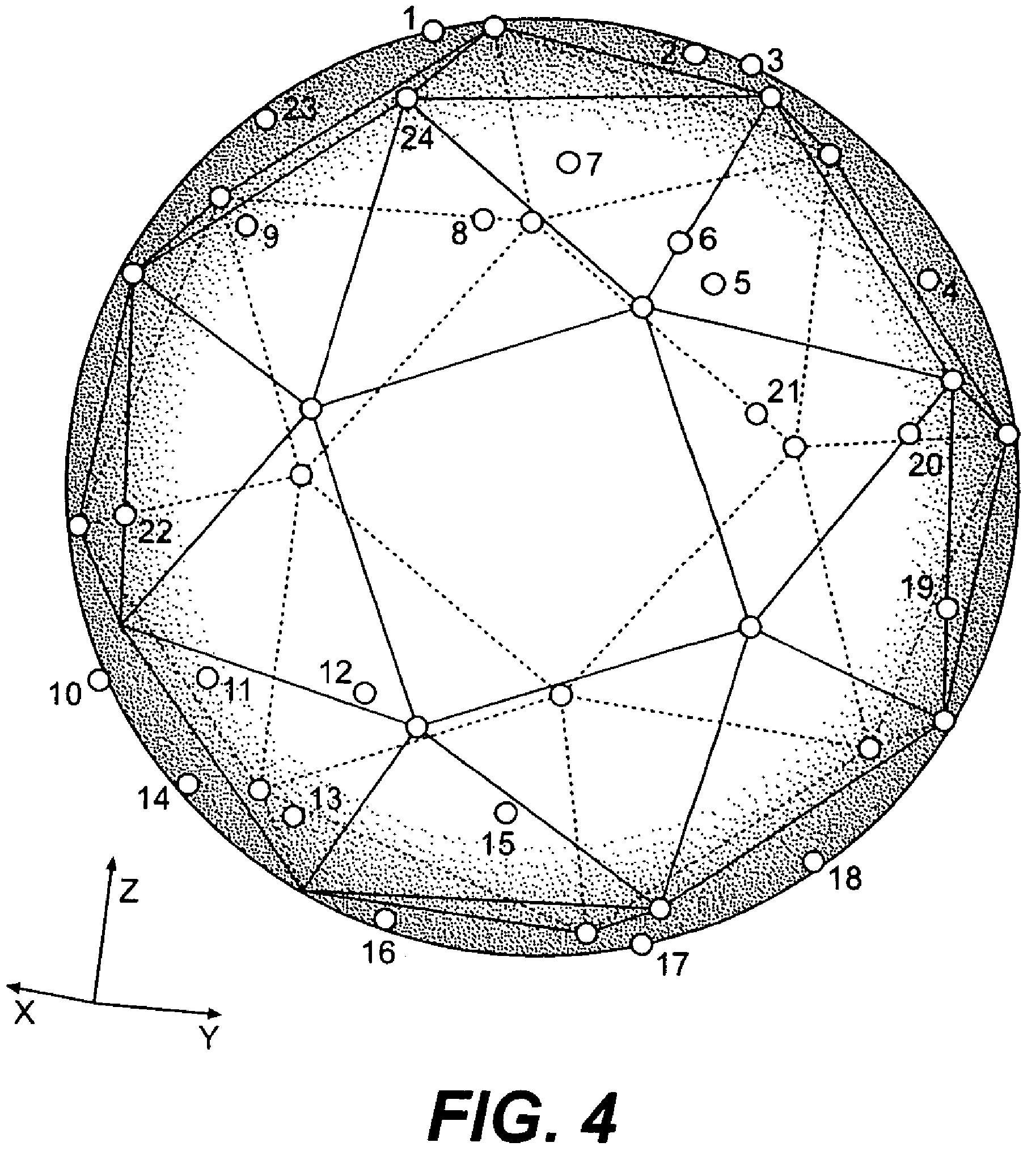
According to another aspect, the present invention comprises a method for arranging a plurality of dimples on a golf ball surface. The method includes defining a first portion of the golf ball surface in which dimples will be arranged, triangulating the first portion of the golf ball surface to form a triangulated surface pattern, generating Soddy circles based on the vertices of the triangulated surface pattern, and positioning dimples based on the Soddy circles.

The method further comprises modifying one or more Soddy circle radii if two or more circles overlap. In one embodiment, the first portion of the golf ball surface comprises the entire surface of the golf ball. In such an embodiment, it may be desirable for the dimple arrangement in the first portion to be repeated on other portions of the golf ball. Generating a dimple pattern based on Soddy circles preferably results in a total dimple coverage that is about 60% or greater.

The dimple pattern may be generated in any desirable manner. Preferably, the triangulation and pattern generated are based on a computer program. In one embodiment, the triangulation comprises generating two or more triangulated surface patterns. The triangles may have any desired properties. For example, the angles of the triangles may compri
se obtuse, oblique, equilateral, or any possible combination thereof. The computer program is preferably capable of randomly generating the triangulated surface pattern. However, other user defined criteria may be input into the computer program that may affect the generated dimple pattern. For example, the triangulated surface pattern may optionally be based on at least one of polyhedra and Archimedean solids.

In one embodiment, it may be desirable to further optimize the dimple pattern generated based on Soddy circles. This may be accomplished, for example, by optimizing the positioning of dimples based on the electromagnetic theory. Optimizing based on the electromagnetic theory includes defining a second portion of the golf ball surface in which dimples will be arranged, placing a first plurality of dimples within the defined surface, and assigning charge values to the dimples. Coulomb’s Law is then applied to determine the potential of the charges. Lastly, a first solution method is applied to minimize the potential, and then the dimple location and distribution according to the solution method may be altered. In some embodiments, there may be regions within the first and second portions where no dimples can be defined. As will be understood by those skilled in the art, the properties of the dimples such as cross section and the like may be varied.

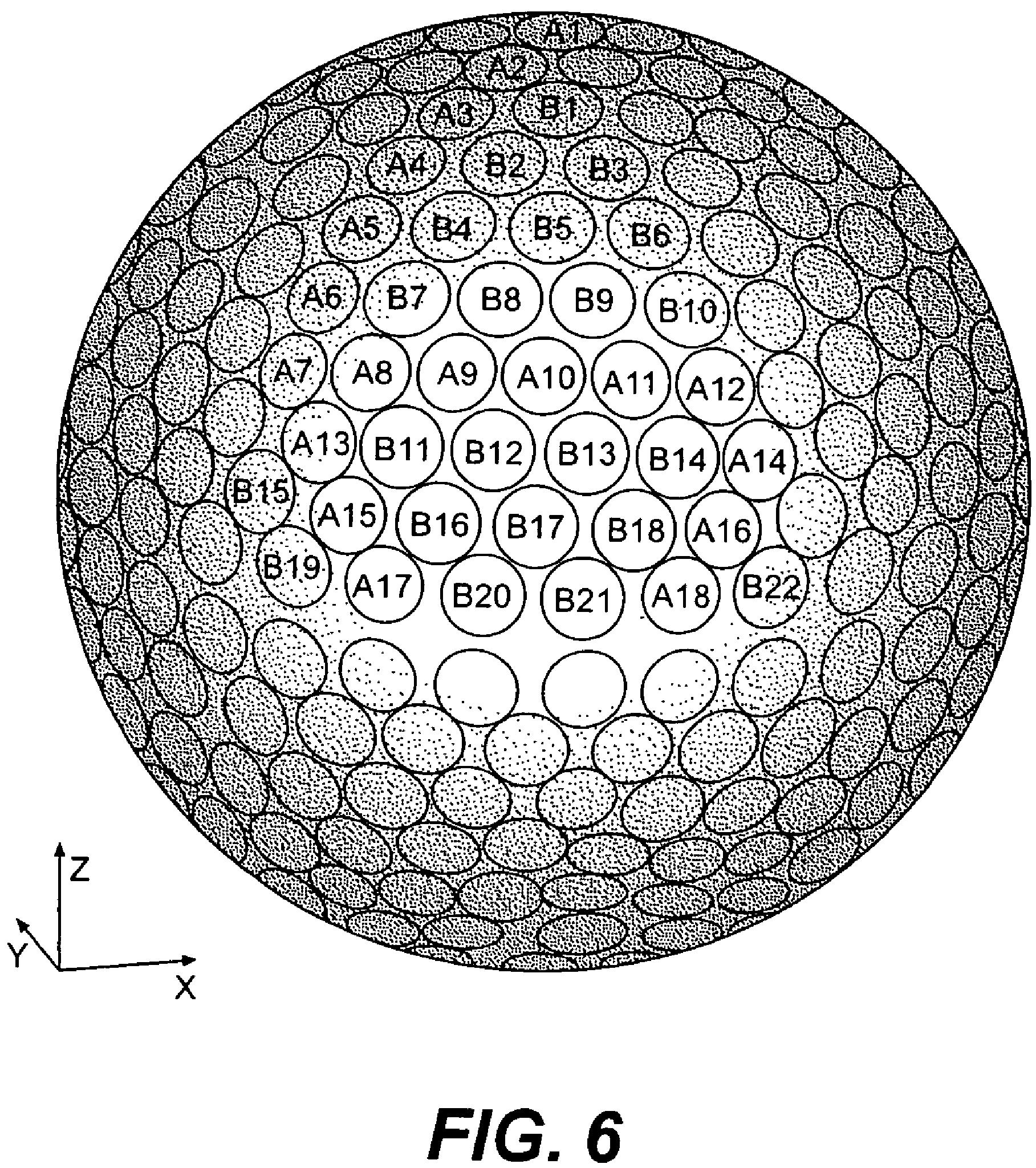
According to another aspect, the present invention comprises a method for arranging a plurality of dimples on a golf ball surface. The method includes defining a first portion of the golf ball surface in which dimples will be arranged and positioning dimples within the first portion based on circle packing. It is desirable for substantially all of the dimples to be mutually tangent to at least three neighboring dimples. However, in other embodiments the circles may be arranged such that at least some of them are mutually tangent.

According to this aspect of the present invention, the dimple pattern may be generated in order to achieve a total dimple coverage of about 80% or more. In one embodiment, the dimple pattern may be generated based on a predetermined number of different circle diameters, or a predetermined number of fixed circle positions. In another embodiment, it may be desirable for the pattern to be generated based on circles having two or more substantially different diameters or circles having substantially similar diameters.

According to an exemplary embodiment, the method may further comprise defining a second portion of the golf ball surface in which dimples will be arranged, triangulating the second portion of the golf ball surface to form a triangulated surface pattern, generating Soddy circles based on the vertices of the triangulated surface pattern, and positioning dimples based on the Soddy circles. In this exemplary embodiment, at least one dimple within the first portion overlaps at least one adjacent dimple within the second portion. When this occurs, the percentage overlap is preferably between about 1% and about 5%, and more preferably between about 2% and about 4%.

I just can’t explain why I find this stuff fascinating! Next time you are on the tee, look at your ball and ask yourself “are those dimples placed on the regions defined by a great rhombicosidodecahedron?”

Dave Dawsey  – Tracking Golf Ball Technology

PS – click here for other golf ball posts